Ниже приводятся четыре простейшие операции над целочисленными значениями, записанные на языке Форт¹: 

+  плюс       ( n1 n2 -- сумма )        сложение  ( n1 + n2 )
-  минус      ( n1 n2 -- разность)      вычитание ( n1 - n2 )
*  звездочка  ( n1 n2 -- произведение)  умножение ( n1 * n2 )
/  слэш       ( n1 n2 -- частное)       деление   ( n1 / n2 )

В отличие от калькулятора на терминале компьютера не предусмотрены специальные клавиши для выполнения операций умножения и деления. Вместо них мы пользуемся клавишами * и /.

Из предыдущего раздела вы уже знаете, что можно сложить два числа, поместив их в стек и выполнив слово +, а затем ., чтобы вывести результат на терминал:

¹ Для нематематиков. Хотя данная глава и напоминает .немного учебник по алгебре, решение математических задач— всего лишь небольшая часть из того, что вы сможете делать с помощью Форта. Позднее вы познакомитесь с другими применениями Форта. Здесь же уместно напомнить, что целые числа — это такие круглые числа, как ... — 3, —2, —1, 0, 1, 2, 3, ,.., а целочисленная арифметика (что достаточно логично) — операции над целыми числами.

17 5 + .  22 ok

Вы можете выполнить таким образом все арифметические операции даже без составления «программы», используя Форт-систему как калькулятор. Решите задачу на умножение:

7 8 * .  56 ok

Как видите, знак операции следует за значениями. Если же вы производите вычитание и деление, необходимо учитывать порядок следования значений («7 — 4» не эквивалентно «4 — 7»).

Запомните следующее правило: для записи выражения в пост-фиксной форме достаточно передвинуть знак операции в конец этого выражения: 

Поэтому чтобы выполнить вычитание

7 - 4 =

наберите на клавиатуре

7 4 - . 3 ok

Для начинающих, которым нравится развлекаться за терминалом. Если вы из тех, кто любит постигать суть вещей, не читая руководства, вы неизбежно столкнетесь с рядом проблем. Во-первых, как уже отмечалось, описанные выше операции являются целочисленными операциями. Это означает не только то, что вы не имеете права их выполнять над дробными числами, например

10.00 2.25 +

но и то, что вы можете получить лишь целочисленный результат, т. е.

21 4 / . 5 ok , а не 5.25 ok

Во-вторых, если вы попытаетесь выполнить умножение: 

10000 10 *

или перемножить подобные большие числа, то получите неожиданный результат. Поэтому мы вас предупреждаем, что все операции, о которых шла речь выше, а также операция, для вывода результата могут выполняться только над числами, лежащими в диапазоне от — 32 768 до 32767. Эти числа называются числами одинарной длины со знаком.

Напомним, что, рассматривая перечень слов Фopтa_, мы употребляли букву n, чтобы обозначить место, где должно находиться число. Так как в Форте числа одинарной длины используются гораздо чаще чисел других типов, вместо п следует подставлять число одинарной длины. Конечно, существуют операции, которые выполняются и над значениями из расширенного диапазона (двойной длины). Они обозначаются буквой d.

Все эти непонятные пока проблемы будут объяснены в свое время, так что не снижайте внимания.

Порядок чисел остается тем же. В качестве примера решите задачу на деление:

20 4 /

Слово / определено таким образом, что нижнее число в стеке делится на число, находящееся в его вершине. 

Как поступить, если необходимо выполнить несколько операций? Например:

4 + (17 * 12)

Как известно, сначала нужно выполнить операцию, указанную в скобках, т. е. 17 умножить на 12, а затем добавить четыре. На Форте это будет выглядеть так:

17 12 * 4 + .  208 ok 

Числа 17 и 12 помещаются в стек. Слово * перемножает их и возвращает результат в стек.

Далее число 4 помещается в стек над числом 204. Слово + «выкатывает» суммирующую машину и складывает эти два числа, а в стек возвращается только результат.

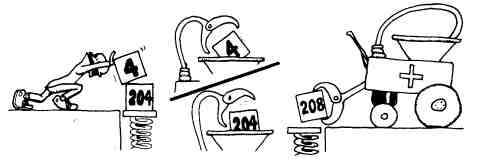
Предположим, вы хотите сложить пять чисел. Вы можете это сделать на Форте, скажем, так:

17 20 + 132 + 3 + 9 + . 181 ok

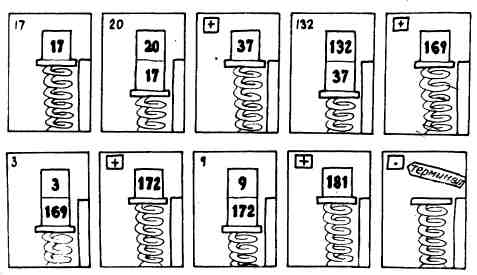
Еще одна интересная задача:

(3+9) * (4+6)

Чтобы ее решить, мы должны сначала сложить числа 3 и 9, затем 4 и 6 и, наконец, перемножить полученные две суммы. На Форте это можно записать следующим образом:

3 9 + 4 6 + *

В результате вы получите.

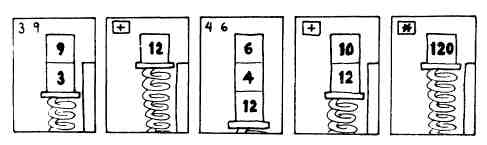
Заметьте, что мы весьма кстати сохранили сумму, равную 12, в стеке на то время, пока складывали числа 4 и 6.

Помните, что мы еще не пишем определений, а лишь используем Форт-систему в режиме калькулятора. Начинающим, возможно, потребуется решить несколько практических задач для того, чтобы чувствовать себя увереннее в применении постфиксной записи.

Для начала представьте выражения из левого столбца в постфиксной записи, используя только карандаш и бумагу. Например, если дано 

ab + c                   2 * 3 + 4                   (10)

У вас должно получиться следующее: 

a  b  *  c  +

Затем проверьте полученные выражения, подставляя в них числа из среднего столбца и применяя Форт в режиме калькулятора. Правильный результат приведен в правом столбце. В нашем случае

2 3 *  4 + . 10 ok

1.  c(a + b)                 3 ( 4 + 5 )             (27)

       ab                      80 * 90
2.    ----                    ---------              (72)
      100                        100

     3a - b                  ( 3 * 9 ) - 7
3.   ------ + c              ------------- + 2       (7)
        4                           4

      a + 1                    7 + 1
4.    -----                    -----                 (2)
        4                        4

5.   x(7x + 5)               10 ((7 * 10) + 5)       (750)  

Преобразуйте следующие выражения из постфиксной формы в инфиксную:

6.   a b - b a + /

7.   a b 10 * /

 Ответы к упражнению 2-A

1.  a b + c *   или   c a b + *
2.  a b * 100 /
3.  3 a * b - 4 / c +
4.  a 1 + 4 /
5.  7 x * 5 + x *
    a - b
6.  -----
    b + a
      a
7.   ---
     100

Как вы уже знаете из первой главы, новые слова можно определять с помощью чисел и ранее определенных слов. Теперь, используя некоторые из изученных нами арифметических операций, рассмотрим другие возможности языка.

Допустим, вы хотите перевести различные единицы измерения в дюймы. Вам известно, что 1 ярд = 36 дюймам и 1 фут = 12 дюймам¹. Поэтому вы можете определить эти два слова следующим образом:

: ЯРД>ДМ ( ярды -- дюймы ) 36 * ; ок
: фУТ>ДМ ( футы -- дюймы ) 12 * ; ок

Здесь определяемые имена означают «ярды-в-дюймы» и «футы-в-дюймы» соответственно. Ниже приводятся примеры выполнения указанных слов:

10 ЯРД>ДМ . 360 ок
2 ФУТ>ДМ . 24 ок

¹ дюйм = 2,54 см, 1 фут = 30,48 см, 1 ярд = 0,914 м. — Примеч. пер.

Если результат должен всегда выражаться в дюймах, то необходимо ввести следующие определения:

: ЯРДОВ ( ярды -- дюймы ) 36 * ; ок
: ФУТОВ ( футы -- дюймы ) 12 * ; ок
: ДЮЙМОВ ( -- ) ; _ok

Таким образом, можно записать выражение:

10 ЯРДОВ 5 ФУТОВ + 9 ДЮЙМОВ + . 429 ок

Отметим, что назначение слова ДЮЙМОВ — напомнит вам, для чего здесь поставлено число 9. Если вы хотите писать грамотно, то должны добавить три определения:

: ЯРД ЯРДОВ ; ок
: ФУТ ФУТОВ ; ок
: ДЮЙМ ; ок

Набирая при вводе эти существительные в единственном числе, вы получите такой же результат:

1 ЯРД 5 ФУТОВ + 1 ДЮЙМ + . 97 ок
6 ЯРДОВ 1 ФУТ + . 228 ok

До сих пор мы вводили слова, определения которых содержали только одну арифметическую операцию. Но с тем же успехом вы можете при необходимости использовать внутри любого определения несколько операций.

Допустим, вы хотите получить слово, которое суммирует пять чисел, находящихся в стеке. Ранее мы уже суммировали пять чисел следующим образом:

17 20 + 132 + 3 + 9 + . 181 ok

однако можно набрать на клавиатуре и такую строку:

17 20 132 3 9 + + + + . 181 ok 

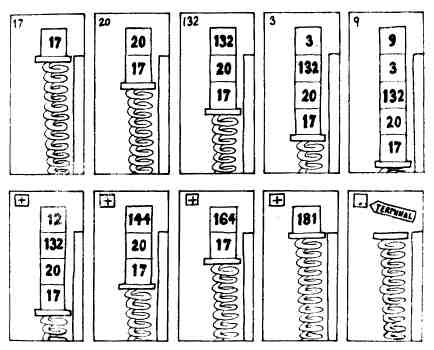
Мы получили тот же ответ, несмотря на то что собрали все числа в одну группу, а все знаки операций — в другую. Запишем наше определение так:

: 5#СУММА ( n1 n2 n3 n4 n5 — сумма ) + + + + ; ок

и выполним слово, как показано ниже:

17 20 132 3 9 5#СУММА . 181 ок

Ниже приводится еще одно выражение, для которого нужно записать определение¹:

(а + b) * с

¹Для начинающих, которым нравятся задачи, сформулированные словесно. Реактивный самолет летит со средней скоростью 600 миль/ч. Скорость попутного ветра составляет 25 миль/ч. Сколько миль пролетит этот самолет при таких условиях за пять часов? Если мы определим слово

: РАССТОЯНИЕ ( время скорость попутный—ветер — расстояние ) + * ;

то можно затем ввести следующее:

5 600 25 РАССТОЯНИЕ . 3125 ок

Попытайтесь выполнить это слово с различными значениями, учитывая и встречный ветер (отрицательные значения).

Как вы видели из упр. 2-А, это выражение может быть записано в постфиксной форме:

с а b + *

Итак, мы можем записать наше определение:

: РЕШЕНИЕ ( с a b — п ) + * ; ок

Преобразуйте следующие выражения из инфиксной формы в форму определений Форта и укажите порядок аргументов в стеке для этих определений. Порядок аргументов в стеке может быть произвольным, но он должен быть наиболее удобным для данного определения, В соответствии с номером упражнения 2-Б вы можете именовать ваши определения как 2Б1 и 2Б2 и т. д. Например: 

1. ab + c примет вид: 2Б1 * + ;
   a - 4b
2. ------ + c
      6
      a
3.  -----
      8b
     0.5ab
4.  -------
      100
5.  a(2a + 3)
    a - b
6.  -----
      c

Ответы к упражнению 2-Б

6. Если вы скажете, что такое выражение преобразовать нельзя, то будете правы, по крайней мере сейчас, пока мы еще не рассмотрели специальных стековых операций.

2. : 2Б2 ( c a b -- x ) 4 * - 6 / + ; 3. : 2БЗ ( a b -- x ) 8 * / ; 4. : 2Б4 ( a b -- x ) * 200 / ; 5. : 2Б5 ( a a -- x ) 2 * 3 + * ;

Слово / (слэш) отображает самую простую операцию деления в Форте. Слэш обеспечивает только частное; если в результате деления образуется остаток, он теряется. Набрав на клавиатуре

22 4 / . 5 ok

вы получите только частное (пять) и не получите остаток (два). Если же вы хотите выполнить операцию деления, аналогичную предусмотренной в карманном калькуляторе, такой результат вас не удовлетворит, тем более что Форт не позволяет даже округлить полученное целое число.

Но / — всего лишь одна из нескольких операций деления в Форте. Такое разнообразие операций дает пользователю широкие возможности. Во многих задачах округленный результат или результат двойной точности вам и не требуется. Допустим, вам нужно решить такую задачу: сколько банкнот достоинством в один доллар получается при размене 22 четвертей доллара? Ответ очевиден: пять (а не 5.5). Машинный меняла, к примеру, не будет знать, как выдать вам 5.5 дол. Здесь необходимы операции, подобные операции /, но вычленяющие целые частное и остаток: 

MOD           ( n1 n2 -- n-остаток )   Деление. В стек помещается
                                       остаток от деления.

/MOD          ( n1 n2 --               Деление.    В стек помещаются
                n—остаток n-частное )  остаток и частное.

Итак, если вам требуется только частное, применяйте операцию /, если вам требуется только остаток — операцию MOD¹, а если и остаток, и частное — операцию /MOD.

Выполним в качестве примера операцию /MOD:

22 4 /MOD . . 5 2 ok

¹Для любознательных. MOD — сокращение от modulo, что означает "остаток".

Полученных вами знаний уже достаточно для того, чтобы легко написать следующий набор определений: 

: ДОЛ-ЧЕТВЕРТИ ( четверти -- четверти доллары ) 4 /MOD ;
: .ДОЛЛАРЫ ( доллары -- ) . ." долларов * ;
: .ЧЕТВЕРТИ ( четверти — ) . ." четверти " ;
: ЧЕТВЕРТИ ( четверти — )
   ДОЛ-ЧЕТВЕРТИ ." Получается" .ДОЛЛАРЫ ." и " .ЧЕТВЕРТИ ;

Далее вы можете ввести

22 ЧЕТВЕРТИ

и получить

22 ЧЕТВЕРТИ Получается 5 долларов и 2 четверти ок

В Стандарте Форт-83 во всех операциях деления частное

Что же делать, если в прикладных программах требуется округление? Не беспокойтесь — нужные средства легко создаются, как вы увидите в разд. «Округление» гл. 5, путем комбинирования и расширения элементарных арифметических операций.

Если вы пытались решить задачу 6 в последнем упражнении, то вам уже ясно, что выражение в инфиксной форме 

    a - b
    -----
      c

нельзя преобразовать в форму определения Форта без того, чтобы каким-то образом не поменять местами значения в стеке. «Каким-то образом» — это значит, что вы должны выполнить операцию преобразования стека, а именно перестановку SWAP.

¹ Для тех, кто имеет склонность к математике. Хотите верьте, хотите нет, но в информатике мы сталкиваемся с противоречиями при решении даже такой простой задачи, как «—32 разделить на 7». Результатом может быть либо —4 при -остатке -3 (-4 х 7 = -28; -28 + — 3 = 31), либо -5 при остатке 4 (-5 х 7 = -35; -35 + 4 = 31). Группа по разработке стандарта Форт-83 приняла решение о том, что при выполнении операций деления частное не должно округляться. Иными словами, дзух целых чисел, между которыми находится дробное частное, выбирается меньшее. В нашем примере -5 меньше, чем -4, поэтому выбирается -5. При делении без округления частного знак остатка совпадает со знаком делителя. Таким образом, если мы делим -31 на 7 в среде Форт-83, то получаем частное -5 и остаток 4, Это правило относится к делению чисел со знаком и не приводит к противоречиям в окрестности нуля.

 SWAP (ПЕРЕСТАНОВКА)

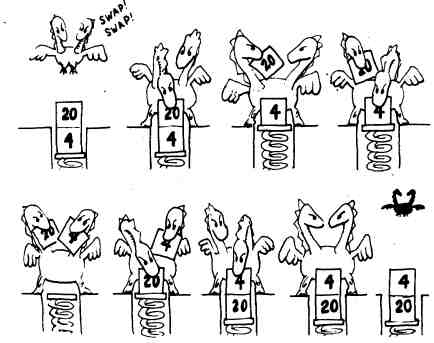
Слово SWAP, определено так, что при его выполнении два верхних элемента стека меняются местами.

Вы можете проверить, как выполняется операция SWAP, а также поэкспериментировать со стеком за своим терминалом в режиме калькулятора, когда это слово не должно появляться внутри определения.

Для начала введите следующее:

1 2 . . 2 1 ok

а затем то же самое, но со словом SWAP:

1 2 SWAP . . 1 2 ok

Теперь задача 6 из упр. 2-Б может быть решена таким образом:

- SWAP /

если содержимое стека определяется как ( c a b -- ).

Присвоим переменным а, b, с контрольные значения: а = 10, b = 4, с = 2. Поместим их в стек и выполним предложение, например такое:

2 10 4 - SWAP / . 3 ok

Ниже приводится список операций работы со стеком:

SWAP	( nl n2 -- n2 nl )	Перестановка двух верхних элементов стека
DUP	( n -- n n )	Дублирование верхнего элемента стека.
OVER	( n1 n2 -- nl n2 n1 )	Копирование второго элемента стека и размещение копии в вершине стека.
ROT	( nl n2 n3 -- n2 n3 n1 )	Размещение третьего элемента в вершине стека.
DROP	( n -- )	Удаление верхнего элемента из стека.

DUP (дублирование)

При выполнении следующей в списке операции над стеком, DUP, просто создается второй экземпляр верхнего элемента стека. Например, если у вас в стеке есть элемент а, то вы можете вычислить а²:

DUP *

При этом выполняются следующие действия:

ОПЕРАЦИЯ	СОДЕРЖИМОЕ СТЕКА
	a
DUP	a a
*	a2

  OVER (ЧЕРЕЗ)

Теперь допустим, что кто-то попросил вас вычислить выражение

а * (а + b)

при следующем содержимом стека:

( a b — )

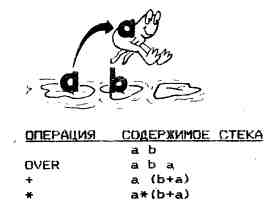
Вы скажете, что для этого потребуется новая операция со стеком, так как вам нужно два экземпляра а, и а должно находиться под b. OVER и есть та самая «новая» операция. OVER создает еще один экземпляр а, который «перепрыгивает», как при игре в чехарду, через b:

Теперь исходное выражение

а * (а + b)

может быть легко записано в виде

OVER + *

При этом происходит следующее: 

Прежде чем записывать выражения на Форте, их нужно разложить на множители. Например, вычислить выражение

а2 + ab

с помощью Форта, применяя только описанные выше средства, довольно сложно (если вообще возможно) до тех пор, пока вы не разложите это выражение на множители, т. е. не приведете его к виду

а * (а + b)

А такое выражение вы уже умеете вычислять

ROT (ПЕРЕМЕЩАТЬ ПО КРУГУ)

Это четвертая операция в нашем списке (ROT — сокращение от rotate). Посмотрите, что происходит при ее выполнении с тремя верхними элементами стека:

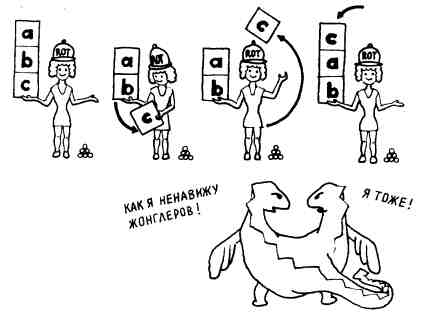
Например, если вам нужно вычислить выражение ab — bс, то сначала необходимо вынести b за скобки:

b(а - с)

а затем, если начальное состояние стека таково:

( с b a — )

можно написать

ROT - *

При этом выполняются следующие действия:

ОПЕРАЦИЯ	СОДЕРЖИМОЕ СТЕКА
	c b a
ROT	b a c
-	b (a - c)
*	(b*(a-c))

 DROP (ИСКЛЮЧИТЬ/УДАЛИТЬ)

Последняя в нашем списке операция со стеком — DROP. Ее назначение состоит в том, чтобы удалить верхний элемент из стека 

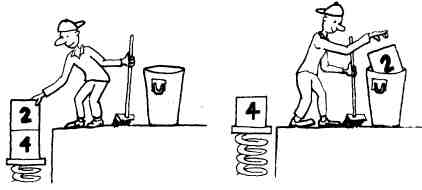
Просто, не правда ли? Позднее мы найдем для этой операции несколько хороших применений.

При отладке программ программисту часто необходимо знать, что в данный момент находится в стеке. Конечно, набрав серию точек, мы выведем на терминал содержимое стека, но при этом выведенные значения будут потеряны для последующих операций В большинстве Форт-систем имеется слово с именем .S, которое для своего выполнения не требует аргументов в стеке и выводит содержимое стека, не разрушая его, т. е. оставляя после завершения функционирования прежнее состояние стека. При отладке программы вы можете ввести несколько слов, выполнить слово .S, чтобы убедиться в том, что содержимое стека соответствует результату функционирования введенных слов, ввести еще несколько слов, снова выполнить .S и т. д.

Давайте проверим: 

1 2 3 .S
1 2 3 ok
ROT .S
2 3 1 ok

При изучении слов манипулирования со стеком начинающие иногда используют следующий прием:

: SWAP SWAP .S ;
: DUP DUP .S ;
: OVER OVER .S ;
: ROT ROT .S ;
: DROP DROP .S ;

Таким образом осуществляется немедленная обратная связь по каждой выполняемой команде. (Это возможно потому, что интерпретатор из двух слов с одинаковыми именами выполняет занесенное в словарь последним.)