
До сих пор речь шла только о числах одинарной длины со знаком. В настоящей главе мы введем числа без знака и числа двойной длины и познакомим вас с новыми операциями над этими числами.
Излагаемый здесь материал разделен на две части. В первой части (для начинающих) рассматриваются числа применительно к компьютеру, а также дается точное определение терминов со знаков без знака, одинарная длина, двойная длина, во второй (для всех) продолжается обсуждение Форта и объясняется, как трактуются числа со знаком и без знака, одинарной и двойной длины (точности).
Все цифровые компьютеры хранят числа в двоичной форме1. Элемент стека Форт-системы состоит из 16 разрядов2, или битов (бит
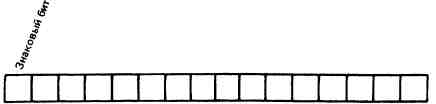
- двоичная цифра). Ниже показана структура из 16 битов, где приводятся значения всех битов:

Если в каждом бите хранится единица, то это число составит 65535. Таким образом, 16 битами можно представить любое значение от 0 до 65535. Поскольку такой способ представления не позволяет нам изображать отрицательные числа, мы называем их числами без знака. В наших таблицах и стековой нотации числа без знака обозначаются буквой и.
1 Для тех, кто не знаком с двоичной системой счисления. Попросите кого-нибудь из ваших друзей (увлекающегося математикой) рассказать вам об этой системе или поищите учебное пособие по ЭВМ для начинающих.
2 Для пользователей 32-разрядных компьютеров. В таких процессорах, как 68000, стек Форта обычно 32-разрядный. Поэтому термин, число одинарной длины в данном случае означает 32-разрядное число.
Но как же быть с отрицательными числами? Чтобы иметь возможность изображать как положительные, так и отрицательные числа, необходимо пожертвовать одним битом, задействовав его под знак. Для этой цели мы отведем самый левый «старший по порядку» бит. 15 оставшихся бит позволят нам представить любое число вплоть до 32767. Если знаковый бит содержит единицу, то нужно отложить изображаемое значение по оси влево от нуля, т. е. в области отрицательных чисел. Таким образом, с помощью 16 бит можно представить число в диапазоне от
-32768 до +32767. Вы уже знаете, что этот диапазон составляют числа одинарной длины, обозначаемые буквой п.
Мы столь подробно останавливаемся на представлении отрицательных чисел, чтобы у вас была полная ясность по всем излагаемым здесь вопросам. У вас может сложиться впечатление, что достаточно просто ввести знаковый разряд, и вы сможете различить отрицательное и положительное числа, однако на самом деле это далеко не так.
Чтобы понять, как представляются отрицательные числа, вернемся снова к десятичной системе счисления и понаблюдаем за показаниями счетчика, устанавливаемого на магнитофонах многих типов. Допустим, что счетчик высвечивает три цифры (трехзначное число). По мере перемотки ленты это число увеличивается. Установим счетчик на нуль и начнем перематывать ленту в обратном направлении. Первое число, которое вы увидите на индикаторе, будет 999. Его мы воспринимаем как
- 1. Следующим числом окажется 998, что соответствует
-2, и т. д.
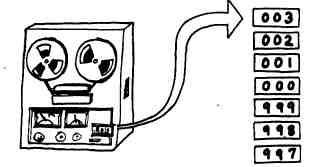
Аналогично представляются числа со знаком и в компьютере. Если мы начнем с нуля:
0000000000000000
и вернемся назад на одно число, то будем иметь
1111111111111111 (16 единиц)
что означает 65535 при изображении чисел без знака и
-1 при изображении чисел со знаком. Число 1111111111111110
соответствует 65534 при изображении чисел без знака и
-2 при изображении чисел со знаком.
(Традиционно числа -1 и 0 применяются в качестве значений «истина» и «ложь» потому, что в представлении -1 все биты установлены, а в представлении 0 - сброшены.)
Ниже приводится схема, в которой показано, каким образом двоичное число в стеке может использоваться как число без знака или как число со знаком.

Такой странный на первый взгляд способ представления отрицательных чисел дает возможность компьютеру использовать одни и те же процедуры для выполнения как вычитания, так и сложения.
Продемонстрируем изложенное на примере простой задачи:
2 - 1 ---
Эта задача эквивалентна задаче сложения 2+
(-1). При двоичном представлении чисел одинарной длины двойка выглядит следующим образом:
0000000000000010
а отрицательная единица - так:
1111111111111111
Компьютер складывает их таким же образом, как мы это делаем на бумаге. Если сумма в какой-то колонке превышает единицу, то в следующую колонку (старший двоичный разряд) переносится 1. В результате получается:
0000000000000010 + 1111111111111111 ----------------- 1000000000000001
Как видите, компьютеру потребовалось выполнить перенос единицы в старший разряд во всех колонках, а последняя единица была вынесена в 17-й разряд. Но так как элемент стека состоит только из 16 битов, будет выведено число 0000000000000001 т. е. единица, что является правильным ответом.
Мы не объясняем здесь, каким образом компьютер переводит положительное число в отрицательное. При желании вы можете найти описание этого процесса, который называется «дополнением до двух», в литературе.
Когда мы рассматривали в гл. 5 выполнение компьютером некоторых арифметических операций, нам встретились две «таинственные» фразы: «арифметический сдвиг влево» и «арифметический сдвиг вправо». Теперь настала пора объяснить их.
От чего зависит быстрота ответа Форт-системы.
2* ( n -- n*2) Умножение на два ( арифметический сдвиг влево). 2/ ( n -- n/2) Деление на два ( арифметический сдвиг вправо).
Для иллюстрации представим какое-нибудь число, скажем шесть, в двоичном виде:
0000000000000110
(4 + 2). Сдвинем каждую цифру этого числа на один разряд влево, а освободившийся бит заполним нулем:
0000000000001100
Мы получили двоичное представление числа 12 (8 + 4), что ровно в два раза больше первоначального числа. Такой способ применим во всех случаях. Если вы переместите каждую цифру числа на одну позицию вправо и заполните освободившийся бит нулем, то в результате всегда получите половину первоначального числа.
При арифметическом сдвиге знаковый разряд не смещается. Иными словами, положительное число остается положительным, а отрицательное - отрицательным при выполнении операций деления и умножения на два. (Сдвиг, при котором вместе с остальными битами сдвигается и старший по порядку бит, называется логическим сдвигом.) Вы должны знать, что компьютер выполняет сдвиг цифр намного быстрее, чем операции обычного деления или умножения. Когда скорость критична, то лучше написать 2*, чем 2 *, и даже может быть лучше написать 2* 2* 2*, чем 8 * - все зависит от конкретной модели вашего компьютера.
Вы, вероятно, уже знаете, что такое число двойной длины. Это число, представление которого занимает 32 бита вместо 16. Двойная длина допускает представление чисел в диапазоне ±2 147 483 647 (т. е. свыше четырех биллионов).
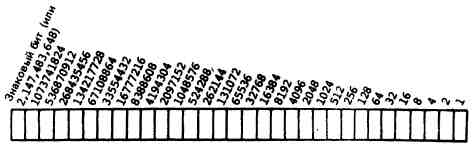
В Форте число двойной длины занимает1 в стеке место двух чисел одинарной длины. Такие операции, как 2SWAP и 2DUP, применимы и для чисел двойной длины, и для пары чисел одинарной длины.
Обращаем ваше внимание на то, что в программировании термином «слово» принято обозначать 16-разрядное число, или два байта. В Форте же под словом понимают некоторым образом определенную команду. Поэтому, чтобы избежать коллизий, программирующие на Форте 16-разрядное значение называют ячейкой. Число двойной длины требует для своего представления двух ячеек.
Как только вы начнете серьезно программировать, вам, кроме двоичной и десятичной систем счисления, понадобятся другие системы, особенно шестнадцатиричная (основание 16) и восьмиричная (основание 8). Позднее мы их подробно рассмотрим, а пока вам не помешает небольшое введение.
Программисты начали использовать шестнадцатиричные и восьмиричные числа потому, что компьютеры «думают» в двоичной системе, а человеку очень трудно воспринимать числа, состоящие из длинного ряда двоичных цифр. Намного проще перевести двоичное число в шестнадцатиричное, чем двоичное в десятичное, поскольку 16 является степенью числа 2, в то время как 10 - нет. То же самое справедливо и для восьмиричной системы. Поэтому программисты обычно применяют для записи двоичных чисел, которыми компьютер обозначает адреса и машинные коды, шестнадцатиричную или восьмиричную системы. Шестнадцатиричная система выглядит на первый взгляд необычно, так как в ней задействованы буквы от А до F.
ДЕСЯТИЧНАЯ ДВОИЧНАЯ ШЕСТНАДЦАТИРИЧНАЯ
0 0000 О
1 0001 1
2 0010 2
3 0011 3
4 0100 4
5 0101 5
6 О11О 6
7 0111 7
8 1000 8
9 1001 9
10 1010 А
11 1011 В
12 1100 С
13 1101 D
14 1110 Е
15 1111 F
Возьмем двоичное число одинарной длины: 0111101110100001. Для того чтобы перевести это число в шестнадцатиричную систему, мы сначала должны разбить его на тетрады: 0111 1011 1010 0001
затем заменить каждую тетраду на ее шестнадцатиричный эквивалент: 7 В А 1 или просто 7ВА1.
В восьмиричной системе используются только цифры от 0 до 7. Большинство современных компьютеров применяет шестнадцатиричную систему, поэтому мы не станем приводить пример на перевод в эту систему. Перевод чисел из одной системы в другую рассматривается более детально в настоящей главе позднее.
Если числа в компьютере хранятся в двоичной форме, то как в нем хранятся буквы или другие символы? Тоже в двоичной форме, только в специальном коде, который был принят в качестве промышленного стандарта много лет назад, ASCII1 (стандартный американский код для обмена информацией). В табл. 7.1 приводятся все символы системы и их цифровые представления как в шестнадцатиричной, так и в десятичной форме.
Символы, помещенные в первом столбце (имеющие шестнадцатиричные коды 0 - 1F), называются управляющими, так как они указывают, что терминал или компьютер должен выполнить, например подать звуковой сигнал, вернуть каретку на одну позицию, начать новую строку и т. д. Остальные символы называются печатными, поскольку они выводят на печать видимые символы, включая буквы, цифры от 0 до 9, все доступные символы и даже пробел (шестнадцатиричный код 20). Единственным исключением является символ DEL (шестнадцатиричный код 7F), который предписывает компьютеру игнорировать последний переданный символ.
В первой главе мы ввели слово EMIT, которое берет из стека значение в коде ASCII и посылает его на терминал для распечатки этого значения в виде символа, например:
65 EMIT A ok 66 EMIT В ok
(Мы используем десятичное, а не шестнадцатиричное представние, потому что ваш современный компьютер больше всего приспособлен ко вводу именно в таком представлении2.)
Почему бы нам не проверить действие EMIT на каждом печатном символе «автоматически»?
: ОТОБРАЖАЕМЫЕ 127 32 DO I EMIТ SPACE LOOP ;
1 Код ASCII совпадает с применяемым в СССР семиразрядным кодом КОИ-7. В реализациях Форта на отечественных ЭВМ используются восьмиразрядные коды (например, КОИ-8) с добавлением кодов русских букв, что и позволяет использовать русские слова. - Примеч ред.
2 Для специалистов Не тратьте время на раздел для начинающих.
Таблица 7.1. Символы в коде ASCII и их числовые эквиваленты
Символ
Шестн
Дес.
Символ
Шестн.
Дес.
Символ
Шестн.
Дес.
Символ
Шестн
Дес.
NUL
00
0
SP
20
32
@
40
64
60
96
SOH
01
1
!
21
33
A
41
65
а
61
97
STX
02
2
"
22
34
В
42
66
b
62
98
ETX
03
3
#
23
35
С
43
67
с
63
99
EOT
04
4
$
24
36
D
44
68
d
64
100
ENQ
05
5
%
25
37
E
45
69
е
65
101
ACK
06
6
&
26
38
F
46
70
f
66
102
BEL
07
7
'
27
39
G
47
71
9
67
103
BS
08
8
(
28
40
H
48
72
h
68
104
HT
09
9
)
29
41
I
49
73
i
69
105
LF
0A
10
*
2A
42
J
4A
74
j
6A
106
VT
0B
11
+
2B
43
К
4В
75
k
6B
107
FF
0С
12
,
2C
44
L
4C
76
l
6C
108
CR
0D
13
-
2D
45
M
4D
77
m
6D
109
SM
0E
14
.
2E
46
N
4E
78
n
6E
110
SI
0F
15
/
2P
47
O
4F
79
o
6F
111
DLE
10
16
0
30
48
P
50
80
p
70
112
DC1
11
17
1
31
49
Q
51
81
q
71
113
DC2
12
18
2
32
50
R
52
82
r
72
114
DC3
13
19
3
33
51
S
53
83
s
73
115
DC4
14
20
4
34
52
Т
54
84
t
74
116
NAK
15
21
5
35
53
U
55
85
u
75
117
SYN
16
22
6
36
54
V
56
86
v
76
118
ETB
17
23
7
37
55
W
57
87
w
77
119
CAN
18
24
8
38
56
X
58
88
x
78
120
EM
19
25
9
39
57
Y
59
89
y
79
121
SUB
1A
26
:
ЗА
58
Z
5A
90
z
7A
122
ESC
1B
27
;
3B
59
[
5В
91
{
7B
123
FS
1C
28
<
3C
60
\
5C
92
|
7C
124
GS
1D
29
=
3D
61
]
5D
93
}
7D
125
RS
1E
30
>
3E
62
^
5E
94
~
7E
126
US
1F
31
?
3F
63
_
5F
95
DEL (RB)
7F
127
В первом столбце перечислены символы в коде ASCII или, если это управляющие символы, в общепринятых обозначениях; в двух последующих столбцах даются их шестнадцатиричные и десятичные эквиваленты
Слово ОТОБРАЖАЕМЫЕ выведет на печать каждый требуемый символ из кода ASCII, т. е. символы с кодами от десятичного 32 до десятичного 126. (Мы используем коды ASCII в качестве индекса цикла DO.)
ОТОБРАЖАЕМЫЕ ! " # $ & ' ( ) * + ... ok
Начинающие могут поинтересоваться, как поведет себя
EMIT с управляющими символами; наберите на клавиатуре такой текст:
Вы услышите какой-то сигнал, который является вариантом звонка печатающей машинки для дисплея. (В некоторых системах слово EMIT вместо того чтобы выполнить команду, выводит специфические символы.)
Неплохо знать следующие управляющие символы:
НАЗВАНИЕ ОПЕРАЦИЯ ДЕСЯТИЧНЫЙ ЭКВИВАЛЕНТ
BS Возврат назад на одну 8
позицию ("забой")
LF Перевод строки 10
CR Возврат каретки 13
Поэкспериментируйте с этими управляющими символами и посмотрите, как они выполняются.
Код ASCII разработан таким образом, что каждый символ в нем может быть представлен одним байтом. В приводимых здесь таблицах буква «с» означает, что содержимое некоторого байта соответствует символу в коде ASCII.
В некоторых Форт-системах имеется слово ASCII, которое используется для улучшения читабельности определений, поскольку переводит отдельные символы в шестнадцатиричные значения. Вспомним, к примеру, следующее определение:
: STAR 42 EMIT ;
Если в вашей системе есть это слово, то вы можете определить его так:
: STAR ASCII * EMIT ;
В обоих случаях элементы словаря после трансляции определений будут абсолютно одинаковы, однако последнее определение легче воспринимается.
ASCII ( -- c) перевод следующего символа из входного
потока в его ASCII-эквивалент
Слова AND и OR (введенные в гл. 4) используют «двоичную логику», т. е. каждый бит проверяется независимо, и перенос единицы в старший разряд не производится. Выполним, например, операцию AND над следующими двумя двоичными числами:
0000000011111111 0110010110100010 AND ---------------- 0000000010100010
Для того чтобы результирующий бит был равен единице, соответствующие биты-аргументы должны быть оба равными единице. Заметьте, что в этом примере первый аргумент содержит все нули в старшем байте и все единицы в младшем. Действие второго операнда здесь заключается в том, что младшие восемь битов сохраняются неизменными, а старшие восемь битов сбрасываются в нуль. Первый операнд служит «маской» для маскирования старшего байта второго операнда.
Слово OR также применяет двоичную логику. В примере
1000100100001001 0000001111001000 OR ---------------- 1000101111001001
единицу получается в тех битах, где хотя бы один операнд был равен единице. И снова каждый столбец проверяется независимо, без переноса единицы в старший разряд. При умелом использовании масок в одном 16-разрядном значении можно хранить 16 отдельных флагов. Так, мы можем узнать, чему равен соответствующий (скажем, пятый) бит: 1011101010011100 нулю или единице, путем маскирования остальных флагов:
1011101010011100 0000000000010000 AND ---------------- 0000000000010000
Так как значение нашего бита равно единице, результат будет истинным. Если бы значение бита составляло нуль, то результат
оказался бы ложным. Мы можем сбросить определенный флаг в нуль, не трогая остальные, следующим приемом:
1011101010011100
1111111111101111 AND
----------------
1011101010001100
^
Мы работали с маской, во всех битах которой, за исключением сбрасываемого в нуль, содержатся единицы. Можно установить тот же самый флаг, т. е. сделать его единицей, таким образом:
1011101010001100
0000000000010000 OR
----------------
1011101010011100
^
Ниже приводятся несколько приемов использования операции AND.
Вы могли заметить, что значение строчной буквы в коде ASCII отличается от значения прописной в точности на 32 (в десятичной системе счисления). Мы можем создать определение, которое осуществляло бы перевод строчного символа в прописной:
: ПРОПИСНОЙ ( строчный-символ -- прописной-символ ) 32 - ;
Итак,
97 EMIT a ok 97 ПРОПИСНОЙ EMIT A ok
К сожалению, данный вариант слова ПРОПИСНОЙ не будет действовать в том случае, если переводимый символ уже является прописным, поскольку весь процесс перевода сводится к простому вычитанию.
Но код ASCII разработан очень мудро. Число 32 выбрано не случайно, а с учетом его представления в двоичной системе счисления. Посмотрите, как выглядят представления прописной и строчной букв А:
A 1000001 a 1100001
Они отличаются только одним битом, который и представляет число 32. Если мы сбросим этот бит в 0, то независимо от того, была ли буква прописной или строчной, она станет прописной:
: ПРОПИСНОЙ ( строчный-символ -- прописной-символ )
95 AND ;
Число 95 является десятичным эквивалентом двоичного числа 1011111
и совпадает с маской для двоичного представления числа 32. Следовательно,
97 ПРОПИСНОЙ EMIT A ok 65 ПРОПИСНОЙ EMIT A ok
(Однако поведение рассматриваемого варианта слова ПРОПИСНОЙ оказывается несколько странным по отношению к небуквенным символам. Попытайтесь, к примеру, перевести цифры.)
Слово XOR также предназначено для работы с битами. Как отмечалось в гл. 4, при выполнении этой операции истина получается только тогда, когда один из аргументов (но не оба сразу) истинен. Сравним результат выполнения операций XOR и OR:
1000100100001001 1000100100001001 0000001111001000 OR 0000001111001000 XOR ---------------- ---------------- 1000101111001001 1000101011000001
Если вы применяете операцию XOR с аргументом, все биты которого равны единице, то тем самым инвертируете биты второго аргумента.
1111111111111111 1000100100001001 XOR ---------------- 0111011011110110
Таким образом, выражение
-1 XOR
является двоичной маской или шаблоном инвертирования. (Существует математический термин дополнение числа до единицы.)
Стандарт-83 и операция NOT Стандарт 83 изменил первоначальный смысл операции NOT В системах, разработанных до принятия этого Стандарта, слово NOT заменяло значение логического аргумента оператора IF противоположным, т е не нуль (истина) становился нулем (ложью) Оно было синонимом слова О.= , созданным для улучшения читабельности программы. В Стандарте-83 слово NOT эквивалентно выражению "-1 XOR" и не сработает в том случае, если значение исходного флага «истина» не представлено как -1.
Обязательно убедитесь в том, что инвертируемое значение является логическим, а не арифметическим. Выражение "0= NOT" вырабатывает из ненулевого значения правильное логическое значение «истина».
В первой главе мы ввели слово NUMBER (ЧИСЛО).

Если слово INTERPRET (ИНТЕРПРЕТАТОР) не может найти введенную строку символов в словаре, то оно передает ее слову NUMBER, после чего NUMBER пытается прочесть всю совокупность символов как двоичное число. Когда NUMBER это удается, прочитанное число помещается в двоичной форме в стек NUMBER не проверяет числа на принадлежность их какому-либо диапазону1, поэтому может представлять вводимые числа либо как числа со знаком, либо как числа без знака. Например, при вводе любого числа в диапазоне от 32768 до 65535 NUMBER представит его в виде числа без знака, а любого значения в диапазоне от -32768 до -1 - как целое в двоичном дополнительном коде. Это важный момент: стек может быть использован для хранения целых чисел со знаком или целых чисел без знака. Будет ли некоторое двоичное значение интерпретироваться как целое со знаком или как целое без знака, зависит от выполняемых над ним операций. Вы выбираете то, что вам больше подходит в данной ситуации, а затем твердо придерживаетесь выбранного варианта.
1 Для начинающих. NUMBER не проверяет, выходит ли введенное вами в качестве числа одинарной длины значение за рамки соответствующего диапазона. Если вы ввели слишком большое число, то NUMBER преобразует его, но сохранит только 16 последних значащих цифр.
Ранее мы ввели слово ., которое выводит на печать из стека значение в виде целого со знаком:
65535 .-1 ok
Слово U. печатает то же самое двоичное представление как число без знака:
6S535 U. 65535 ok
U. ( u -- ) Вывод числа одинарной длины без знака с
одним пробелом после него.
Напоминаем, что буквой n обозначаются числа одинарной длины со знаком, а буквой u - числа одинарной длины без знака.
Ниже приводятся еще два слова, использующие числа без знака:
U.R ( u ширина -- ) Вывод числа без знака. Число выровнено
по правой границе поля заданной ширины.
U< ( u1 u2 -- ? ) Помещение на стек истины в том случае,
если u1<u2. Оба аргумента рассматриваются
как числа одинарной длины без знака.
После загрузки Форт-системы все преобразования чисел как для ввода, так и для вывода осуществляются в десятичной системе счисления.
Применив перечисленные ниже команды, вы можете сменить текущую систему счисления:
HEX ( -- ) - устанавливает шестнадцатиричную систему счисления;
OCTAL ( -- ) - устанавливает восьмиричную систему счисления
(применяется в некоторых системах);
DECIMAL ( -- ) - возвращает десятичную систему.
Вновь принятая система счисления остается таковой до следующего изменения, так что не забудьте объявить DECIMAL, как только закончите работать с другой системой счисления.
Рассмотренные команды упрощают преобразования чисел при работе в режиме калькулятора. Если требуется, к примеру, перевести число 100 в шестнадцатиричную систему, вы должны ввести следующее:
DECIMAL 100 HEX . 64 ok
Для того чтобы перевести шестнадцатиричное число F в десятичную систему (помните, что вы уже имеете дело с шестнадцатиричной системой), нужно ввести:
0F DECIMAL . 15 ok
Возьмите себе в привычку с этого момента предварять каждое шестнадцатиричное значение нулем, например:
0А 0B 0FF
что позволит отличать их от системных слов, таких, как В в словаре РЕДАКТОРА (EDITOR).
Полезный прием. Определение двоичной (BINARY) или любой другой системы счисления. Начинающие, которые хотят посмотреть, как выглядят числа в двоичной системе, могут ввести следующее определение:
: BINARY 2 BASE ! ;
Новое слово BINARY выполняется так же, как и OCTAL или HEX, но изменяет текущую систему счисления на двоичную. В тех системах, где нет слова OCTAL, в порядке эксперимента можно определить:
: OCTAL 8 BASE ! ;
Числа двойной длины составляют диапазон ±2147483647. Большинство Форт-систем до некоторой степени поддерживают работу с числами двойной длины. Для того чтобы вводимое вами (с клавиатуры или из блока) число воспринималось в стеке как число двойной длины, проще всего включить в состав этого числа десятичную точку. Например, когда вы вводите:
200000.<return>
NUMBER воспринимает запятую как признак того, что данное значение должно быть представлено числом двойной длины и помещает это значение в стек в виде двух последовательных ячеек (ячейкой в Форте называется структура из 16 битов), причем старшая по порядку ячейка помещается над младшей1.
Слово D. выводит число двойной длины без всяких знаков пунктуации:
D. ( d - ) Печать числа двойной длины со знаком.
Здесь d - целое число двойной длины со знаком. Например, если вы введете число двойной длины, а затем выполните операцию D., то компьютер вам ответит:
D. 200000 ok
В некоторых Форт-системах для выделения дробной части применяются еще четыре знака пунктуации:
, / - :
В таких системах все перечисленные ниже числа переводятся в одно и то же представление:
12345. D. 12345 ok 123.45 D. 12345 ok 1-2345 D. 12345 ok 1/23/45 D. 12345 ok 1:23:45 D. 12345 ok
1 Для специалистов. В большинстве Форт-систем положение десятичной точки запоминается в некоторой переменной, и вы можете это использовать в своих целях. Более подробную информацию вы найдете в документации по вашей системе. Мы продолжим обсуждение данного вопроса в гл. 10 (см. «Преобразование чисел при вводе»).
Кроме того, в некоторых системах, где применяются арифметические сопроцессоры, на расширенное представление целого числа указывает не десятичная точка, а символ X, например:
123456789X
а число -12345 - нет, потому что оно будет представлено как отрицательное число одинарной длины. (Это единственный случай, когда дефис интерпретируется как минус, а не как знак пунктуации.)
Далее мы покажем, как вы можете определить свой собственный эквивалент операции D., чтобы выводить вместе с числом любой знак пунктуации.
Приведенные ниже слова:
8200.00 12/31/86 372-8493 6:32:59 98.6
иллюстрируют типы форматов вывода, которые вы можете создать, определив ваши собственные слова «форматного вывода» Форта. Рассмотрим этот вопрос подробнее.
Самое простое определение форматного вывода вы можете написать следующим образом:
: UD. ( ud -- ) <# #S #> TYPE ;
UD. предназначено для вывода числа двойной длины без знака. Слова <# и #> (СКОБКА-ЧИСЛО и ЧИСЛО-СКОБКА) означают начало и конец процесса преобразования числа. В данном определении весь перевод осуществляется единственным словом #S (ЧИСЛА). #S преобразует значение из стека в символы кода ASCII. По этой команде формируется столько цифр, сколько их необходимо для представления числа: незначащие нули она не выводит. Однако всегда выводится по крайней мере одна цифра: если значение равно нулю, то выводится нуль, например:
12,345 UD. 12345ok 12, UD. 12ok 0. UD. 0ok
Слово TYPE (ПЕЧАТЬ) выводит символы, которые составляют число. Заметьте, что между числом и приглашением ok нет пробела. Для того чтобы вывести пробел, вы должны просто добавить слово SPASE, как это сделано в приведенном ниже примере:
: UD. ( ud -- ) <# #S #> TYPE SPACE ;
Предположим, что у вас в стеке имеется номер телефона, выраженный 32-разрядным целым числом, скажем 372-8493 (помните, что дефис указывает NUMBER на то, что число нужно воспринимать как значение двойной длины. В вашей системе это может быть точка). Вы хотите определить некоторое слово, которое будет представлять такое число снова в виде телефонного номера. Назовем его .ТЕЛЕФОН (для вывода номера телефона) и запишем следующее определение:
: .ТЕЛЕФОН ( ud - )
<# # # # # 45 HOLD #S #> TYPE SPACE ;
Ваше определение .ТЕЛЕФОН содержит все компоненты слова UD. и некоторые другие. Слово Форта #(ЧИСЛО) выводит только одну цифру. Определение форматного вывода числа берет цифры выводимого числа в обратном порядке, поэтому выражение «# # # #» выводит четыре крайние правые цифры номера телефона. Теперь самое время вставить дефис. В таблице значений кода ASCII (см. часть I - для начинающих) дефис закодирован десятичным числом 45. Слово Форта HOLD (ЗАНЕСТИ) возьмет этот код ASCII и вставит его в строку символов форматируемого числа.
Если в вашей системе имеется слово ASCII, то вы можете заменить в приведенном выше определении непонятное выражение "45 HOLD" на более читабельное:
ASCII - HOLD
Слово ASCII {которое мы ввели в первой части данной главы) помещает в стек числовое значение следующего символа из входного потока, в нашем случае - дефис.
Итак, у вас остались три левые цифры. Вы можете воспользоваться выражением «# # #», но проще применить слово #S , которое автоматически приведет остаток вашего числа к требуемому виду.
Последовательность <#...#>> называется выражением форматного вывода числа, поскольку формирует шаблон (справа налево), по которому число должно быть сформатировано.

Теперь представим число двойной длины без знака как календарную дату: 7/15/86. Определение будет выглядеть так:
: .ДАТА ( ud -- )
<# # # ASCII / HOLD # # ASCII / HOLD # # #> TYPE SPACE ;
Проследим за тем, как выполняется приведенное выше определение, но будем помнить, что операции обработки чисел в нем расположены в порядке, обратном выводу этих чисел. Выражение
# # ASCII / HOLD
(вы можете вместо "ASCII /" использовать 47) выводит две крайние правые цифры (год) и крайний слэш. При следующем вхождении этого выражения выводятся две средние цифры (день) и левый слэш. Наконец, "# #" выводит две крайние цифры (месяц). Вы можете определить:
: /nn ( ud -- ud) # # ASCII / HOLD ; : .ДАТА ( ud -- ) <# /nn /nn # # #> ТУРЕ SPACE;
Поскольку вы сами управляете процессом преобразования чисел, можно на самом деле переводить различные числа из одной системы счисления в другую. Это может пригодиться вам при форматном выводе времени (часов и минут). Например, у вас в стеке время записано в секундах, а вы хотите определить слово, которое выражало бы это время в часах, минутах и секундах. Определение в данном случае может выглядеть следующим образом1:
: SEXTAL 6 BASE ! ; : :00 ( ud -- ud) # SEXTAL # DECIMAL ASCII : HOLD ; : СЕКУНДЫ <# :00 :00 #S #> TYPE SPACE ;
Для форматного вывода секунд и минут вы используйте слово :00. Как секунды, так и минуты вычисляются по модулю 60, значит, правой цифрой может быть любая цифра до девяти, а левой - цифра от нуля до пяти включительно. Поэтому в своем определении :00 вы преобразуете первую цифру (она является правой) как десятичное число, затем переходите по слову SEXTAL в шестиричную систему (с основанием 6) и преобразуете левую цифру, после чего возвращаетесь в десятичную систему и вставляете символ двоеточия. После того как слово :00 преобразует секунды и минуты, #S переведет оставшиеся часы. Так, если у вас в стеке время задано как 4500 с, то в результате вы получите:
4500. .СЕКУНДЫ 1:15:00 ok
1 Для начинающих. См. полезный прием, описанный на с. 164.
(Если продолжительность дня измерять в секундах, то 86400 с - это слишком много для 16-разрядного числа.)
В табл. 7.2 сведены слова Форта, использующиеся при форматизации чисел. (Обратите внимание на условные обозначения в конце таблицы, которые напоминают вам о смысле символов "n", "d" и т. д.)
Таблица 7.2
Форматирование чисел
<# Начало процесса преобразования числа. В стеке должно находиться
число двойной длины без знака
# Преобразование одной цифры и помещение ее в выходную символьную
строку. # доставляет цифру в ЛЮБОМ СЛУЧАЕ - если вы подали этому
слову на вход неверное цифровое значение, то и в этом случае вы
получите нуль для каждого #
#S Преобразование числа (цифры за цифрой) до тех пор, пока в результате
не получится нуль. Всегда доставляется по крайней мере одна цифра
(нуль, если число равно нулю)
с HOLD Вставка в форматируемую символьную строку на текущую позицию символа,
значение которого в коде ASCII находится в стеке
n SIGN Вставка знака "-" в выходную строку в том случае, если третье число
в стеке отрицательное (это число из стека выбирается - см. сноску
в следующем разделе)
#> Завершение преобразования числа и помещение в вершине стека счетчика
символов и адреса (именно эти аргументы требуются для TYPE)
ВЫРАЖЕНИЕ СОСТОЯНИЕ СТЕКА ТИП АРГУМЕНТОВ
<# ... #> ( d -- а u) или 32-разрядный без знака
( u 0 - а и) 16-разрядный без знака
<# ... ( |d| -- а u) 32-разрядный со знаком,
n SIGN #> где |d| является абсолют-
или мым значением d, a n -
верхней ячейкой d
( |n| 0 -- а u) 16-разрядный со знаком,
где |n| - абсолютное значение n
Условные обозначения: n, n1 ... - 16-разрядные числа со знаком; а - адрес; d, d1 ... - 32-разрядные числа со знаком; u, u1 ... - 16-разрядные числа без знака; с - значение символа в коде ASCII.
До сих пор мы форматировали только числа двойной длины без знака Xoтя структура <#...#> применима именно к таким числам, попробуем воспользоваться ею и для других типов чисел, выполнив определенные манипуляции со стеком. Например, рассмотрим простейший вариант системного определения D. (оно выводит число двойной длины со знаком):
: D. ( d -- ) DUP >R DABS <# #S R> SIGN #> TYPE SPACE ;
Слово SIGN, которое должно располагаться внутри выражения форматного вывода, вставляет знак "-" в строку символов лишь в том случае, если верхний символ в стеке является отрицательным. Следовательно, мы должны сохранить копию верхней ячейки (содержащей знак) в стеке возвратов для дальнейшего использования.
Так как <# требует наличия лишь чисел двойной длины без знака, мы должны взять абсолютное значение нашего числа двойной длины со знаком с помощью слова DABS. Теперь расположение аргументов в стеке соответствует выражению форматного вывода. Затем #S осуществляет перевод цифр справа налево, после чего мы заносим в стек знак. Если этот знак отрицательный, то SIGN добавляет к форматированной строке минус1. Так как нам нужно, чтобы знак минус располагался слева, включаем SIGN справа в структуру <;#..#!>. В некоторых случаях, например в бухгалтерских расчетах, может потребоваться вывод отрицательных чисел в виде 12345-. В подобной ситуации мы должны поместить слово SIGN слева в выражение <# ...#:>, как показано ниже:
<# SIGN #S #>
1 Для пользователей более ранних систем. Слово SIGN имеет свою историю. Первоначально в качестве аргумента этого слова выступал третий элемент стека. Таким образом, для того чтобы определить слово D., нужно было писать
: D. ( d -- ) SWAP OVER DABS <# #S SIGN #> TYPE SPACE ;
Выражение "SWAP OVER" помещает копию верхней ячейки (той, что со знаком) на дно стека. Чтобы упростить выражение форматного вывода, операцию ROT решено было перенести в определение слова SIGN.
Данное соглашение действовало в системах фиг-Форт и системах полиФорт, разработанных до введения Стандарта-83. В системах Форт-79 и Форт-83, а также Форт-системах МУР и MMS используется соглашение о передаче знака через вершину стека, что в большей степени соответствует механизму передачи данных через стек.
Если вы располагаете старой версией, определите SIGN следующим образом:
: SIGN ( n -- ) 0< IF ASCII - HOLD THEN ;
Определим слово, которое выводило бы число двойной длины со знаком с десятичной точкой и двумя десятичными значениями после точки. Поскольку такая форма часто используется для представления какой-либо суммы в долларах и центах, назовем это cлово .$ и определим его следующим образом:
: .$ ( d -- ) DUP >R DABS <# # # ASCII . HOLD #S R> SIGN ASCII S HOLD #> TYPE SPACE ;
Проверим его:
2000.00 .$ $2000.00
или даже так:
2,000.00 .$ $2000.00
Рекомендуем вам сохранить определение .$, которое пригодится нам в дальнейшем в некоторых примерах.
Вы можете также описать форматы чисел одинарной длины. Например, если вы хотите использовать число одинарной длины без знака, то просто поместите в стеке перед словом <# нуль. Такое число одинарной длины легко превратить в число двойной длины, которое настолько мало, что его часть, содержащаяся в верхней по порядку ячейке, равна нулю,
Для представления числа одинарной длины со знаком вам достаточно поместить нуль в старшую по порядку ячейку. Но вы также должны сохранить копию числа со знаком для SIGN и, кроме того, оставить абсолютное значение этого числа во втором элементе стека. Все необходимые действия выполняет следующее выражение:
( n -- ) DUP >R ABS 0 <# #S R> SIGN #>
Ниже приводятся «стандартные» выражения, которые применяются для вывода различных видов чисел:
СЛОВУ <# ПРЕДШЕСТВУЕТ
ВЫВОДИМОЕ ЧИСЛО ВЫРАЖЕНИЕ
32-разрядное без знака (ничего)
31-разрядное плюс знак DUP >R DABS
(чтобы сохранить знак в третьем
элементе стека для SIGN)
16-разрядное без знака 0
(чтобы получить фиктивную,
старшую по порядку, часть)
15-разрядное плюс знак DUP >R ABS 0
(чтобы сохранить знак)
Слова для выполнения операций над числами двойной длины имеются не во всех Форт-системах. В некоторые системы они включены на правах выборочных, т. е. прежде чем ими пользоваться, вы должны их загрузить.
Ниже приводится перечень слов двойной длины для выполнении математических операций.
D+ ( dl d2 -- d-сумма) Сложение двух 32-разрядных чисел.
D- ( dl d2 -- d-разность) Вычитание одного 32-разрядного
числа ив другого (dl-d2).
DNEGATE ( d -- -d) Изменение знака 32-разрядного
числа на противоположный.
DABS ( d1 -- |d|) Занесение в стек абсолютного
значения 32-разрядного числа.
DMAX ( d1 d2 -- d-max) Занесение в стек максимального
из двух 32-разрядных чисел.
DMIN ( d1 d2 -- d-min) Занесение в стек минимального
из двух 32-разрядных чисел.
D= ( d1 d2 -- ?) Занесение в стек истины в случае
равенства d1 и d2.
D0= ( d -- ?) Занесение в стек истины, если
d равно нулю.
D< ( d1 d2 -- ?) Занесение в стек истины, если
dl меньше d2.
DU< ( ud1 ud2 -- ?) Занесение в стек истины, если
ud1 меньше ud2. Оба числа без знака.
D.R ( d ширина -- ) Вывод 32-разрядного числа со
знаком. Число выравнивается справа
внутри поля заданной ширины.
Буква D в начале каждого выражения означает, что указанная операция может выполняться только над числами двойной длины, а цифра 2 в начале слова, в частности 2SWAP и 2DUP, - что данная операция может выполняться как над числами двойной длины, так и над парами чисел одинарной длины. Пример выполнения операции D+ :
200000. 300000. D+ D. 500000 ok
В следующей таблице перечислены часто используемые слова Форта, которые выполняются над комбинацией чисел одинарной и двойной длины1:
UM* ( ul u2 -- ud) Перемножение двух 16-разрядных чисел.
Все значения без знака. (В предыдущих
версиях данная операция называлась U*)
UM/MOD ( ud u1 -- u2 u3) Деление 32-разрядного числа на
16-разрядное. В стек заносятся
16-разрядные остаток и частное ( честное в вершину).
Частное округлено до ближайшего меньшего целого!
Все значения без знака. (В предыдущих версиях
данная операция называлась U/MOD).
M* ( n1 n2 -- d- Перемножение двух 16-разрядных чи-
произведение) сел. Все знамени» со знаком.
М+ ( d n -- d-сумма) Сложение 32-разрядного и 16-раэрядного чисел.
Результат 32-разрядный.
М/ ( d n -- n-частное) Деление 32-разрядного числа на 16-разрядное.
Результат 16-разрядный. Все значения со знаком.
М*/ ( d n u -- d) Умножение 32-разрядного на 16-разрядное и
деление промежуточного результата тройной
длины на 16-разрядное число (d*n/u).
Результат 32-разрядный.
Слово UM* является командой быстрого умножения, где под результат отводится 32 разряда. Эта команда может быть использована как базовая при определении других операций умножения. Аналогичным образом все команды деления могут быть определены через базовую операцию UM/MOD.
Ниже приводится пример выполнения операции М+:
200,000 7 М+ D. 200007 ok
С помощью операции М*/ мы можем переопределить наш прежний вариант слова % так, что оно будет выполняться с аргументом двойной длины:
: % ( d n% -- d) 100 M*/ ;
1 См. сноску в разд. «Операции деления» (гл. 2).
Например:
200.50 15 % D. 3007 ok
Если вы загрузили определение „J6 (которое мы приводили ранее), то можете ввести следующий текст:
200.50 15 % .$ $30.07
Можно переопределить данное выше определение R% таким образом, чтобы получать округленный результат двойной длины
: R% ( d n% -- d) 10 M*/ 5 M+ 1 10 M*/ ;
и тогда
200.50 15 R% .$ $30.08
Заметим, что М*/ является единственным «штатным» словом Форта, которое осуществляет умножение аргумента двойной длины. Для того чтобы умножить, скажем, 200000 на 3, мы должны подставить единицу в качестве фиктивного делителя:
200,000 3 1 M*/ D. 600000 ok
так как 3/1 эквивалентно 3.
М*/ также является единственным словом Форта, которое осуществляет деление с результатом двойной длины. Так, при делении 200000 на 4 мы должны подставить единицу в качестве фиктивного числителя:
200,000 1 4 M*/ D. 50000 ok
Если в определении содержится число, например,
: БОЛЬШЕ-НА-ДВАДЦАТЬ ( n - n+20) 20 + ;
то это число компилируется в словарь в двоичной форме точно также, как оно выглядит в стеке.

Двоичное значение числа зависит от системы счисления, которая существует в системе на момент компиляции данного определения. Например, при вводе
HEX : БОЛЬШЕ-НА-ДВАДЦАТЬ ( n -- n+20) 14 + ; DECIMAL
словарное определение должно содержать шестнадцатиричное значение 14, что соответствует десятичному значению 20(16 + 4). Впредь слово НЕСКОЛЬКО-БОЛЬШЕ будет всегда добавлять к содержимому стека эквивалент десятичного числа 20, независимо от текущей системы счисления. В том случае, когда вы поместите слово HEX внутрь определения, основание системы счисления будет изменяться при выполнении данного определения. Например, если вы определяете:
DECIMAL : ПРИМЕР HEX 20 . DECIMAL ;
то число компилируется как двоичный эквивалент десятичного числа 20, поскольку во время компиляции текущей была DECIMAL (десятичная) система счисления. Во время выполнения произойдет следующее:
ПРИМЕР 14 ok
Наше число выдается в шестнадцатиричной системе.
Заметьте, что число, помещенное внутри некоторого определения, называется литералом. (В отличие от слов, присутствующих в этом определении, которые ссылаются на другие определения, значение числа заключено в самом числе.)
Ниже приводится перечень слов Форта, рассмотренных в настоящей главе.
U. ( u -- ) Вывод числа одинарной длины без знака с
одним пробелом после него.
U.R ( u ширина -- ) Вывод числа без знака. Число выровнено
по правой границе поля заданной ширины.
U< ( u1 u2 -- ? ) Помещение на стек истины в том случае,
если u1<u2. Оба аргумента рассматриваются
как числа одинарной длины без знака.
Стековая нотация для форматирования чисел:
ВЫРАЖЕНИЕ СОСТОЯНИЕ СТЕКА ТИП АРГУМЕНТОВ
<# ... #> ( d -- а u) или 32-разрядный без знака
( u 0 - а и) 16-разрядный без знака
<# ... ( |d| -- а u) 32-разрядный со знаком,
n SIGN #> где |d| является абсолют-
или мым значением d, a n -
верхней ячейкой d
( |n| 0 -- а u) 16-разрядный со знаком,
где |n| - абсолютное значение n
Операции над числами двойной длины:
D+ ( dl d2 -- d-сумма) Сложение двух 32-разрядных чисел.
D- ( dl d2 -- d-разность) Вычитание одного 32-разрядного
числа ив другого (dl-d2).
DNEGATE ( d -- -d) Изменение знака 32-разрядного
числа на противоположный.
DABS ( d1 -- |d|) Занесение в стек абсолютного
значения 32-разрядного числа.
DMAX ( d1 d2 -- d-max) Занесение в стек максимального
из двух 32-разрядных чисел.
DMIN ( d1 d2 -- d-min) Занесение в стек минимального
из двух 32-разрядных чисел.
D= ( d1 d2 -- ?) Занесение в стек истины в случае
равенства d1 и d2.
D0= ( d -- ?) Занесение в стек истины, если
d равно нулю.
D< ( d1 d2 -- ?) Занесение в стек истины, если
dl меньше d2.
DU< ( ud1 ud2 -- ?) Занесение в стек истины, если
ud1 меньше ud2. Оба числа без знака.
D.R ( d ширина -- ) Вывод 32-разрядного числа со
знаком. Число выравнивается справа
внутри поля заданной ширины.
Смешанные операции:
UM* ( ul u2 -- ud) Перемножение двух 16-разрядных чисел.
Все значения без знака. (В предыдущих
версиях данная операция называлась U*)
UM/MOD ( ud u1 -- u2 u3) Деление 32-разрядного числа на
16-разрядное. В стек заносятся
16-разрядные остаток и частное ( честное в вершину).
Частное округлено до ближайшего меньшего целого!
Все значения без знака. (В предыдущих версиях
данная операция называлась U/MOD).
M* ( n1 n2 -- d- Перемножение двух 16-разрядных чи-
произведение) сел. Все знамени» со знаком.
М+ ( d n -- d-сумма) Сложение 32-разрядного и 16-раэрядного чисел.
Результат 32-разрядный.
М/ ( d n -- n-частное) Деление 32-разрядного числа на 16-разрядное.
Результат 16-разрядный. Все значения со знаком.
М*/ ( d n u -- d) Умножение 32-разрядного на 16-разрядное и
деление промежуточного результата тройной
длины на 16-разрядное число (d*n/u).
Результат 32-разрядный.
Условные обозначения:
n, n1 ... - 16-разрядные числа со знаком; а - адрес; d, d1 ... - 32-разрядные числа со знаком; u, u1 ... - 16-разрядные числа без знака; с - значение символа в коде ASCII.
Арифметический сдвиг влево и вправо. Процесс сдвига всех разрядов числа, за исключением знакового, влево или вправо для эффективного выполнения операций деления и умножения на степень числа 2 с сохранением знака.
ASCII. Стандартизованная система представления вводимых или выводимых символов в виде побайтных значений. Полное
название - стандартный американский код для обмена информацией.
Байт. Стандартный термин для обозначения 8-разрядного значения.
Восьмиричная система. Система счисления по основанию 8.
Двоичная система. Система счисления по основанию 2.
Десятичная система. Система счисления по основанию 10.
Дополнение. Число, равное исходному по абсолютной величине, но с противоположным знаком. Для того чтобы вычислить разность 10 - 4, компьютер сначала определит дополнение 4 (т. е. -4), а затем произведет сложение 10+ (-4).
Знаковый разряд. Разряд, который для чисел со знаком указывает, является ли данное число положительным или отрицательным, а для чисел без знака является старшим значащим разрядом.
Литерал. Число или символ, значение которого заключено в нем самом; в Форте - это число, появляющееся внутри определения.
Маска. Значение, которое может быть «наложено» на другое значение, в результате чего определенные разряды маскируются, а высвечиваются только интересующие нас разряды.
Слово. В Форте - это определенный элемент словаря, во всех других случаях - это термин для обозначения 16-разрядного значения.
Форматизация чисел. Процесс представления двоичного числа выводимыми на дисплей символами, как правило, в специальной форме, например: 3/13/81 или '£47.93.
Число без знака. Число, которое по определению положительное.
Число одинарной длины без знака. Целое, значение которого может лежать в диапазоне от 0 до 65535.
Шестнадцатиричная система. Система счисления по основанию 16.
Ячейка. Термин Форта для 16-разрядного значения.
7.1. Вероника Вэйнрайт не могла вспомнить верхнее значение для чисел одинарной длины со знаком. У нее не было книги, по которой она могла бы справиться, а была только Форт-система, поэтому она написала определение N-MAX с использованием цикла BEGIN ... UNTIL. После выполнения этого определения у нее получилось следующее:
32767 ok
Восстановите написанное ею определение.
7.2. (Данное упражнение позволит вам приобрести навыки работы с битами.) Прежде всего, если вы не сделали этого ранее, определите слово BINARY.
а) Разряды внутри 16-разрядной ячейки нумеруются с 0 до 15 справа налево, так что нулевым разрядом является самый младший бит, а 15-м - самый старший.
Определите слово с именем БИТ, которое переводило бы номер разряда (от 0 до 15) в маску, соответствующую этому разряду, например 0 бит соответствует маске 1, бит 1 - маске 2, бит 3 - маске 4 и т. д. (Совет: проще всего использовать цикл DO.)
б) Пусть в стеке находится значение, представляющее некоторый массив из 16разрядов (назовем его «битовый!»). Определите слово с именем УСТАНОВИТЬ-БИТ, которое устанавливало бы в единицу заданный бит в массиве «битовый!» при следующей стековой нотации: (битовый! номер-бита - битовый2). Например, если в стеке находится битовый шаблон, равный двоичному числу 1000, и вы выполняете последовательность команд 1 УСТАНОВИТЬ-БИТ (в десятичной системе), то получите в результате 1010.
в) Определите слово ОЧИСТИТЬ-БИТ, которое сбрасывает заданный бит. Стековая нотация та же, что и для слова УСТАНОВИТЬ-БИТ. Например:
BINARY 11111111 DECIMAL 5 ОЧИСТИТЬ-БИТ 7 ОЧИСТИТЬ-БИТ BINARY U. 101011111
г) Определите слово ДАЙ-БИТ, вносящее в стек указанный бит (выбранный посредством маски из массива «битовый»), который мог бы служить аргументом оператору IF (т. е. если бит установлен в единицу, то в стек помещается значение «истина», если нет, - «ложь»). Стековая нотация выглядит следующим образом: (битовый номер-бита - бит). Например:
BINARY 1001 DECIMAL DUP 0 ДАЙ-БИТ . 1 ok DUP 1 ДАЙ-БИТ . 0 ok 3 ДАЙ-БИТ . 8 ok
д) Определите слово с именем ПЕРЕКЛЮЧИТЬ-БИТ с той же стековой нотацией, что и для слов УСТАНОВИТЬ-БИТ и ОЧИСТИТЬ-БИТ, которое переключало бы заданный бит (устанавливало бы его в единицу, если бы он был сброшен, и наоборот).
е) Пусть заданы две битовые последовательности, причем вторая получена путем изменения значений нескольких битов первой. Определите слово с именем ИЗМЕНЕНИЕ, которое воспроизводило бы битовую маску с измененными битами.
7.3. Напишите определение, которое заставило бы зазвонить колокольчик на вашем терминале три раза Убедитесь в том, что перерыв в звучании достаточен для того, чтобы отдельные звонки не слились в один длинный звонок. Всякий раз при звучании колокольчика на экране терминала должно появляться слово БИП.
Упражнения 7.4 и 7.5 посвящены выполнению операций над числами двойной длины.
7.4 а) Перепишите созданные в гл. 5 определения перевода значений температур из одной шкалы в другую в предположении, что вводимые в результирующие значения температур должны быть представлены целыми числами двойной длины со знаком с коэффициентом масштабирования 10 (т. е. должны быть умножены на 10). Например, если вы вводите фактическое значение 10.5°, то оно будет представлено 32-разрядным целым числом со значением 105.
б) Напишите слово для форматного вывода с именем .ГРАДУСЫ, которое будет выдавать 32-разрядное целое с коэффициентом масштабирования 10 как строку цифр с десятичной точкой и одной дробной цифрой. Например:
12.3 .ГРАДУСЫ<return> 12.3 ok
в) Преобразуйте следующие значения температур:
0.0 °F в °С 212.0 °F в °С 20.5 °F в °С 16.0 °С в °F -40.0 °С в °F 100.0 °К в °С 100.0 °К в °F 233.0 °К в °С 233.0 °К в °F
7.5, а) Напишите программу, которая вычисляет значение полинома 7х2 + 20х + 5 при заданном х и выводит результат в виде числа двойной длины.
б) Какое максимальное значение может принимать х, чтобы при вычислении результата как 32-разрядного числа со знаком не произошло переполнения?
7.6. Неопытный пользователь экспериментирует с шестнадцатиричными числами и пытается вернуться снова к десятичной форме, вводя команду DEC. Несмотря на то что Форт-система выводит ok, пользователю кажется, что перевод из одной системы счисления в другую не происходит. Что случилось?
7.7. Напишите слово, которое бы выводило числа от 0 до 16 (десятичных) в десятичной, шестнадцатиричной и двоимой системах счисления в три столбца, т. е.
DECIMAL 0 HEX 0 BINARY 0 DECIMAL 1 HEX 1 ВINARY 1 DECIMAL 2 HEX 2 BINARY 10 ... DECIMAL 16 HEX 10 BINARY 10000
7.8. Введите число 37 и дважды выполните команду . (точка). Объясните, что вы получили и почему. Введите число Ь5536. и дважды выполните команду . . Объясните результат. Попытайтесь ввести число 65538. (с десятичной точкой).
7.9. Если вы вводите
..<return>
(две точки, не разделенные пробелом) и система отвечает вам ok, что это означает? 7.10. Напишите определение для форматного вывода номера телефона, которое одновременно выводит через слэш номер района тогда и только тогда, когда в этот номер включен номер района, т. е.
555-1234 .ТЕЛЕФОН 555-1234 ok 213/372-8493 .ТЕЛЕФОН 213/372-6493 ok
(В некоторых системах вместо слэша и дефиса может быть выведена десятичная
точка )